LUAS SEGI-n BERATURAN, JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA, GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN

  NAMA : EVA MARDIANA

KELAS : X MIPA 3

ABSEN : 12

LUAS SEGI-n BERATURAN, JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA, GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN

Pada dasarnya bangun datar segi-n beraturan terbentuk dari lingkaran yang dibagi-bagi menjadi beberapa bagian yang sama besar (berbentuk segitiga sama kaki). Sehingga untuk menghitung luas dan keliling bangun datar segi-n kita akan melibatkan sudut pusat dan jari-jarinya. Sudut pusatnya adalah sudut pada segitiga dengan besarnya adalah yang ditunjukkan oleh tanda sudut warna 360°/ n yang ditunjukkan oleh tanda sudut warna merah. Sementara sisi dari bangun datar segi-n ditunjukkan oleh huruf x.

Rumus Luas Segi - n Beraturan

Segi-n beraturan yaitu bangun datar atau bentuk dimensi 2 yang terdiri dari garis-garis bersambungan membentuk bangun tertutup dengan  sisi yang sama panjang dan  sudut yang sama besar.

 
Jumlah besar sudut dalam segi-n beraturan dapat ditentukan dengan rumus : 

Jumlah besar sudut dalam  segi-n : (n-2) x 180°  

contoh :

•  Jumlah besar sudut dalam segitiga =(3-2) x 180°= 180° 
• Jumlah besar sudut dalam segiempat =(4-2) x 180°=360° 
• Jumlah besar sudut dalam segilima =(5-2) x 180°=540°

Jumlah besar setiap sudut segi-n beraturan dapat ditentukan dengan rumus : 

Jumlah besar setiap sudut segi-n : (n-2) x 180° / n 

contoh : 

• Jumlah besar setiap sudut segitiga =(3-2) x 180° / 3 =60°  
• Jumlah besar setiap sudut  segiempat = (4-2) x 180° / 4 =90°
• Jumlah besar setiap sudut segilima =(5-2) x 180° / 5 =108°                                                                                                                                                                                                                         

Contoh Soal Segi n Beraturan

1. Tentukan luas segi 12 beraturan yang jari jari lingkaran luarnya memiliki panjang 9 cm?

Pembahasan.
Diketahui : r = 9 cm ; n = 12
Ditanyakan : Luas = ?

Jawab :
Luas = n/2 r² sin 360º/n
          = 12/2 x 9² x sin 360º/12
          = 6 x 81 x sin 30º
          = 6 x 81 x ½ 
          = 243 cm²

Jadi luas segi 12 beraturan tersebut ialah 243 cm².

Segi-n beraturan dalam lingkaran :

Lingkaran luar segitiga adalah lingkaran yang dibentuk dari perpanjangan garis bagi tiga sisi segitiga dan kelilingnya akan tepat menyinggung tiga titik sudut segitiga yang ada di dalamnya.

Pada gambar diatas, terdapat sebuah segitiga ABC dengan dengan sisi a,b, dan c. Ada lingkaran luar yang berpusat di titik O yang mengitari segitiga tersebut. OA, OB, OC. dan OD masing-masing adalah jari-jari lingkaran luar yang akan kita cari rumusnya. Untuk membantu menemukan rumus jari-jari, kita memakai garis bantu yaitu garis tinggi segitiga CT dan garis diameter yang ditarik dari titik C (garis CD).

Coba sobat perhatikan ΔCAD dengan ΔCTB

∠CAD = ∠CTB = 90o (ingat sifat sudut keliling yang menghadap diameter sama dengan 90º)

∠ADC = ∠TBC (ingat bahwa dua sudut keliling yang menghadap busur lingkaran yang sama adalah sama besar)

Karena ada dua pasang sudut yang sama maka bisa disimpulkan bahwa ΔCAD dan ΔCTB sebagung (kongruen). Karena sebangun maka perbandingan sisi-sisinya akan sama.

BC/CD = CT/AC
CD (diameter) = BC x AC / CT
CD (diameter) = a x b / CT……. (persamaan 1)

Nilai CT bisa kita cari dengan persamaan Luas

Luas ΔABC = 1/2 AB x CT
2 Luas ΔABC = AB x CT
CT = 2 Luas ΔABC / AB
CT = 2L/ c……..(persamaan 2)

Kita masukkan persamaan 2 ke persamaan 1

CD = a x b / CT
CD = a x b / (2L/c)
CD = a x b x c / 2L

Jari-jari = 1/2 CD
r = 1/2 CD = a x b x c / 4L

a,b,dan c = sisi-sisi segitiga
L = luas segitiga

Lingkaran Dalam Segitiga

Cara membuat lingkaran dalam segitiga , buatlah garis bagi simetris dari masing-masing segitiga. Garis bagi adalah garis yang membagi sudut segitiga tersebut sama besar. Bagaimana cara membuat garis bagi akan kita bahas nanti). Dari titik perpotongan ketiga garis bagi tersebut dapat dibuat sebuah lingkaran. Titik potong ketiga garis bagikan menjadi pusat lingkaran dan kelilingnya akan tepat menyinggung masing-masing sisi segitiga.

Jari - Jari Lingkaran Dalam

Perhatikan gambar di atas, jari-jari lingkaran yang akan kita cari adalah OE = OF = OD. Ketiganya sama dengan tinggi dari segitiga 1, 2 dan 3.

Luas Segitiga Besar = Luas ΔI + Luas ΔII + Luas ΔIII

——————-  = 1/2 (AB x OD) + 1/2 ( CB x OE) + 1/2 (AC x OF)

——————-  = 1/2 (AB x r) + 1/2 (CB x r) + 1/2 (AC x r)

——————-  = 1/2 r (AB + CB + C)

——————-  = 1/2. r. Keliling Segitiga (setengah keliling bisa dilambangkan dengan s?)

——————-  = r. S

Jadi L = r . S

r = L/S

Jadi, jari-jari lingkaran dalam dapat dicari dengan membagi luas segitiga dengan 1/2 kelilingnya. Sekarang bagaimana mencari luas segitiganya? Karena segitiga di atas adalah segitiga sembarang sobat bisa menggunakan rumus

Jadi rumus jari-jari lingkaran dalam menjadi:

dengan

L = Luas Segitiga
S = 1/2 keliling Δ = 1/2 (a + b + c)

Rumus di atas tergantung jenis segitiga. Kalau segitiga siku-siku akan lebih enak mencari luasnya dengan rumus 1/2 alas kali tinggi daripada menggunakan s.

GARIS SINGGUNG  PERSEKUTUAN DALAM & LUAR

1. Rumus Garis Singgung Persekutuan Dalam Dua Buah Lingkaran. 

Yang dimaksud adalah panjang ruas garis yang dibentuk oleh titik-titik singgung lingkaran dengan garis singgung persekutuan dalam. 

Perhatikan gambar!!

Gambar di atas menunjukkan lingkaran P dan lingkaran Q yang secara berturut-turut memiliki panjang jari-jari r1 dan r2. Garis RT merupakan garis singgung persekutuan dalam dari lingkaran-lingkaran P dan Q. Apabila ruas garis RT digeser ke atas sejauh PT sedemikian sehingga titik T berimpit dengan P dan menghasilkan ruas garis SP maka SP = RT, dan SR = PT = r1. Perhatikan bahwa SQ = SR + RQ = PT + RQ = r1 + r2, dan jarak antara titik-titik pusat lingkaran-lingkaran P dan Q adalah d. Karena segitiga QSP siku-siku di S, maka berlaku teorema Pythagoras sebagai berikut :

Kesimpulan dari pembahasan diatas = Kuadrat dari panjang garis singgung persekutuan dalam lingkaran sama dengan kuadrat dari jarak titik-titik pusat kedua lingkaran dikurangi dengan kuadrat dari jumlah panjang jari-jarinya.

Contoh Soal :

Diketahui dua buah lingkaran dengan jarak kedua pusat lingkaran 15 cm, jari-jari lingkaran besar 5 cm, dan jari-jari lingkaran kecil 4 cm. Tentukan panjang garis singgung persekutuan dalamnya?

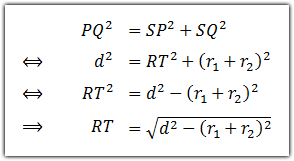
Penyelesaian :

PQ = d = 15cm

r2   = 5

r1    = 4

RT = √(d2 – ( r1+ r2 )2)

     = √(152 – ( 4+ 5 )2)

     = √(225 - ( 9 )2)

     = √(225 - 81)

     = √144

     = 12

2. Rumus Garis Singgung Persekutuan Luar Dua Buah Lingkaran.

Misalkan lingkaran A dan lingkaran B berikut secara berturut-turut memiliki jari-jari yang panjangnya r1 dan r2, seperti diperlihatkan oleh gambar berikut ini.

Garis DC di atas merupakan garis singgung persekutuan luar dari lingkaran A dan lingkaran B. Apabila Ruas garis DC digeser ke bawah sejauh CE sedemikian sehingga titik D berimpit dengan titik A, maka DC = AE dan DA = CE. Perhatikan bahwa EB = CB – CE, dan misalkan AB = d.

Karena segitiga AEB siku-siku di E, maka berlaku teorema Pythagoras seperti berikut:

Karena AE = DC, AB = d, dan EB = CB – CE  = r2 – r1 maka diperoleh kesimpulan bahwa

Kuadrat dari panjang ruas garis singgung persekutuan luar dua lingkaran sama dengan kuadrat dari jarak titik pusat kedua lingkaran dikurangi dengan kuadrat dari selisih jari-jarinya.

Contoh Soal :

Diketahui dua buah lingkaran dengan jarak kedua pusat lingkaran 26 cm, jari-jari lingkaran besar 12 cm, dan jari-jari lingkaran kecil 2 cm. Tentukan panjang garis singgung persekutuan dalamnya?

Jawab :

AB = d = 26cm

r2   =12

r1    =2

RT = √(d2 – ( r1- r2 )2)

     = √(262 – ( 12- 2 )2)

     = √(676 - ( 10 )2)

     = √(676 - 100)

     = √576

     = 24